Week 13:
Spatial Data and
Project 3 Introduction

Agenda

Spatial data overview

Spatial joins

Project 3 overview

Before we start, let’s recap…

In unit 1, we learned about time series data.

• The tool to analyze time series data is time series decomposition and forecasting.

In unit 2, we learned about cross-sectional data.

• The tool to analyze cross-sectional data is cluster analysis.

…and here’s where we’re going.

In unit 3, we will learn about panel data.

• The tool to analyze panel data is regression analysis.

Panel data is a combination of time series and cross-sectional data, where we observe multiple units over multiple time periods.

On our way to regression analysis

Before we get to regression, we’ll take a short detour into spatial data.

Why?

• Many panel datasets include geographic identifiers (like zip codes or counties).

• To work with these, we need to know how to connect (i.e., join) different layers of spatial information (like store locations to zip codes).

• This week’s tool: spatial joins.

To use spatial joins, we need to know what kind of spatial data we’re working with.

What is spatial data?

Data about a point or area defined in space.

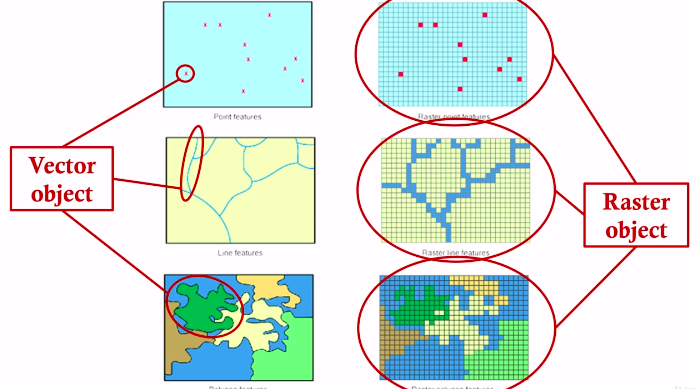
Vector Data

• Point (e.g., locations of stores, geotagged tweets)

• Line Data (e.g., roads, rivers)

• Polygon Data (e.g., boundaries of countries, lakes)

Raster Data

• Grid/raster data is reported in a uniformly sized grid over some area (e.g., satellite images)

Common Sources of Spatial Data

• Public datasets (e.g., USGS, NASA)

• Private sources (e.g., Google Maps)

• Crowdsourced data (e.g., PurpleAir)

Understanding Spatial Relationships

Concepts of Spatial Relationships

• Distance and proximity

  • Spherical distance

• Topology (e.g., adjacency, containment)

• Accessibility and connectivity

• Calculating distances between points on a globe requires accounting for the curvature of the earth.

Tools for Analyzing Spatial Relationships

• Geographic Information Systems (GIS)

  • ESRI ArcGIS

  • QGIS (free GUI alternative)

  • R/Python libraries (scripted)

• Spatial functions in databases (e.g., PostGIS)

Working with Spatial Data

Data Collection Techniques

• GPS data collection

• Remote sensing and aerial photography

• Digitizing from paper maps or other datasets

• Public datasets (e.g., Census, USDA Cropland Data Layer)

• GPS devices record location information based on satellite triangulation. There are many applications: your phone uses this to help you navigate; on wildland fires, trained analysts record the location of built fire line.

• Remote sensing and imaging are data generated by satellite mounted instruments: taking digital images; infrared heat detection to characterize emerging fire locations.

Data Processing and Cleaning

• Geocoding and reverse geocoding

• Calculating distance between objects

• Calculating area of polygons

• Spatial joins

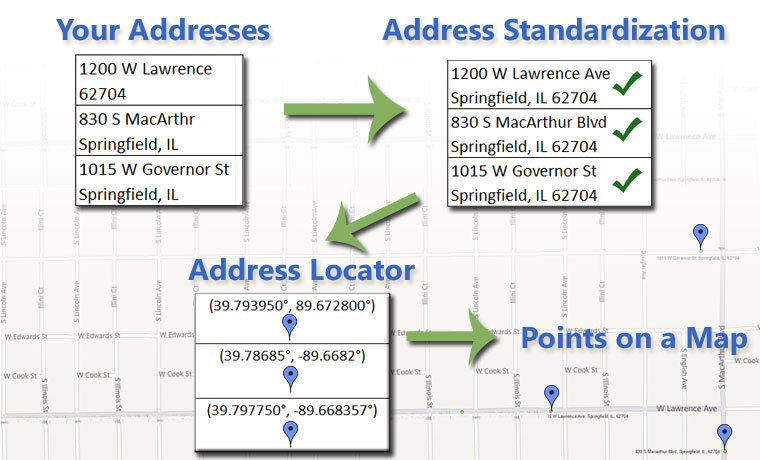
Geocoding and Reverse Geocoding

• Geocoding: Converting an address to a set of coordinates

• Reverse Geocoding: The process from coordinates to address

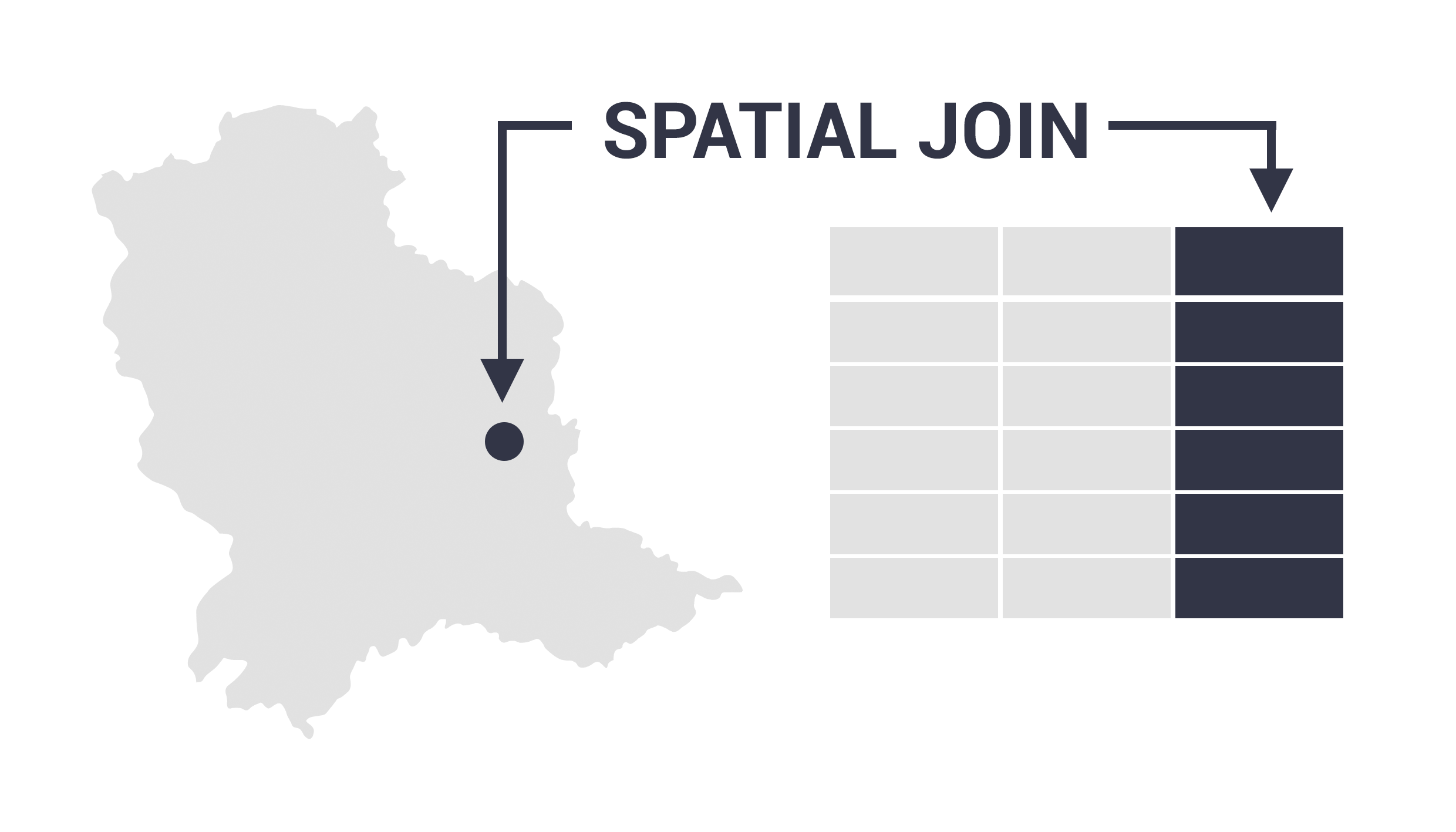
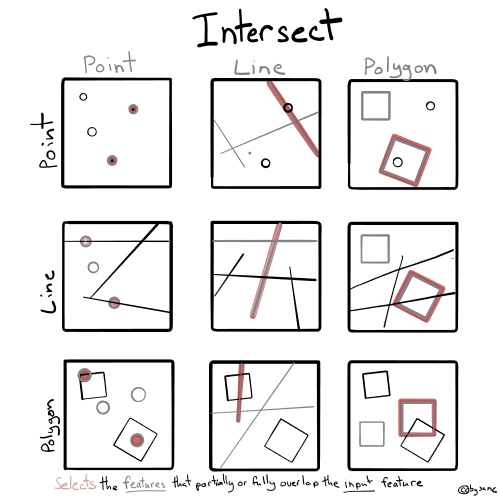
Spatial Joins

• Joining data based on shared location

• Point to point

• Points/lines to polygons

• Polygon to polygon (intersecting polygons)

Takeaways

• Spatial data references a location

• Spatial data enables calculation and manipulation

• Spatial information enables joining to other data (e.g., census)

Lab This Week

• Read and process spatial data in R

• Join spatial data

• Prepare data for mapping in Tableau

Project 3

The Question

The goal of this project is for you to apply panel data analysis to answer a real world question.

This is also a chance to showcase your creativity and analytic skills, putting everything together that you have learned over the semester.

The Data

For this project, you will use the convenience store data (shopper_info, store_info, gtin) to select your \(y\), and choose one of the two additional datasets (census data or weather data) to choose your \(x\).

• Option 1: Convenience store data and Demographic data from the US Census

• Option 2: Convenience store data and Weather data from NOAA

Bringing It Together

Your question for project 3 should be in the form of: What is the association between \(x\) (an explanatory variable) and \(y\) (some outcome)?

1. Choose one of the two options.

2. Based on your question, determine the outcome (\(y\)) to evaluate from the convenience store data.

3. Identify the controls (e.g., weather, population density) that you want to include. This (or these) will serve as your treatment or exposure variable(s), \(x\).

• Including control variables in the regression explains a portion of the variation in your data leaving your variable of interest to explain the remaining variation.

You are responsible for merging or joining your datasets. This means that you must identify the unit of analysis in your datasets and aggregate data to the common unit of analysis.

Example Questions

Using Census

• What is the correlation between population size and total store count at the zip code level?
• What is the association between the number of convenience store locations and median income within a county?
• What is the association between the number of energy drinks sold and the average age of individuals living in a county?

Using Weather

• What is the correlation between total daily rain fall and packaged beverages sales at Allsups locations in Texas?
• What is the correlation between the total daily rain fall and total sales in an area?