Reading layer `tl_2022_us_primaryroads' from data source
`C:\Users\lachenar\OneDrive - Colostate\Documents\GitProjectsWithR\csu-arec-330.github.io\materials\unit_03\week_03\tl_2022_us_primaryroads\tl_2022_us_primaryroads.shp'
using driver `ESRI Shapefile'
Simple feature collection with 17389 features and 4 fields
Geometry type: LINESTRING
Dimension: XY
Bounding box: xmin: -158.1042 ymin: 17.97417 xmax: -65.64866 ymax: 61.57123
Geodetic CRS: NAD83Week 15:
Regression Analysis Example and Course Summary
Agenda
Project overview emphasizing connection between questions and analysis
Economics research example
Course recap
Project Overview
The Question: Your question for Project 3 should be formulated as: What is the association between \(x\) (an explanatory variable) and \(y\) (some outcome)?
The Data: You will use the convenience store data (shopper_info, store_info, gtin) to select your \(y\), and choose one of the two additional datasets (census data or weather data) to choose your \(x\).
Option 1: Convenience store data combined with Demographic data from the US Census
Option 2: Convenience store data combined with Weather data from NOAA
How to succeed for Project 3
Review the lab notes from Week 14
Convey to us that you can turn your question into a model
Spend time interpreting your results
Understanding Gas Prices in Our Community:
A Town Hall Discussion
Introduction
Good evening. I’m Lauren, a local economic analyst.
We’re here today because the community needs to consider adding a new access road to Highway 101.
There is room in the town’s budget for infrastructure improvements, but there is a concern that developing new roads might lead to higher fuel costs.
Tonight, I’ll present to you analysis my team and I conducted on how gas prices vary with distance to the highway.
Goal: To better understand the trade-offs involved with improving highway access so that you, the town planning committee, can decide to add a new access road.
The Question
How does the distance to the nearest highway relate to the price of gas paid by consumers?
Understanding this relationship can help predict expected costs to consumers and manage the town’s budget more effectively.
Background
Concerns about re-routing the highway:
Could create more traffic for the town
Could lead to an increase in gas prices (gas stations could charge a higher price due to proximity to the highway)
Benefits about re-routing the highway:
Shorter commuting time for residents
Better-conditioned road which offers ancillary benefits
More tax revenue from more gas sales
Data Collection
We gathered data from U.S. convenience stores with gas stations.
We calculated their distance to the nearest highway and removed stores located further than 40 kilometers away.
Summary Statistics
Below is a summary table of average prices per gallon and distances from the nearest highway for our sample of gas stations.
Table 1: Summary Statistics for Unit Price and Distance
| Mean | SD | Min | Max | |
|---|---|---|---|---|
| Price Per Gallon | 3.49 | 0.36 | 2.50 | 5.00 |
| Distance | 14.75 | 68.72 | 0.00 | 2,346.76 |
Distribution of Unit Price and Distance
Figure 1: Matrix of density plots for unit price and distance
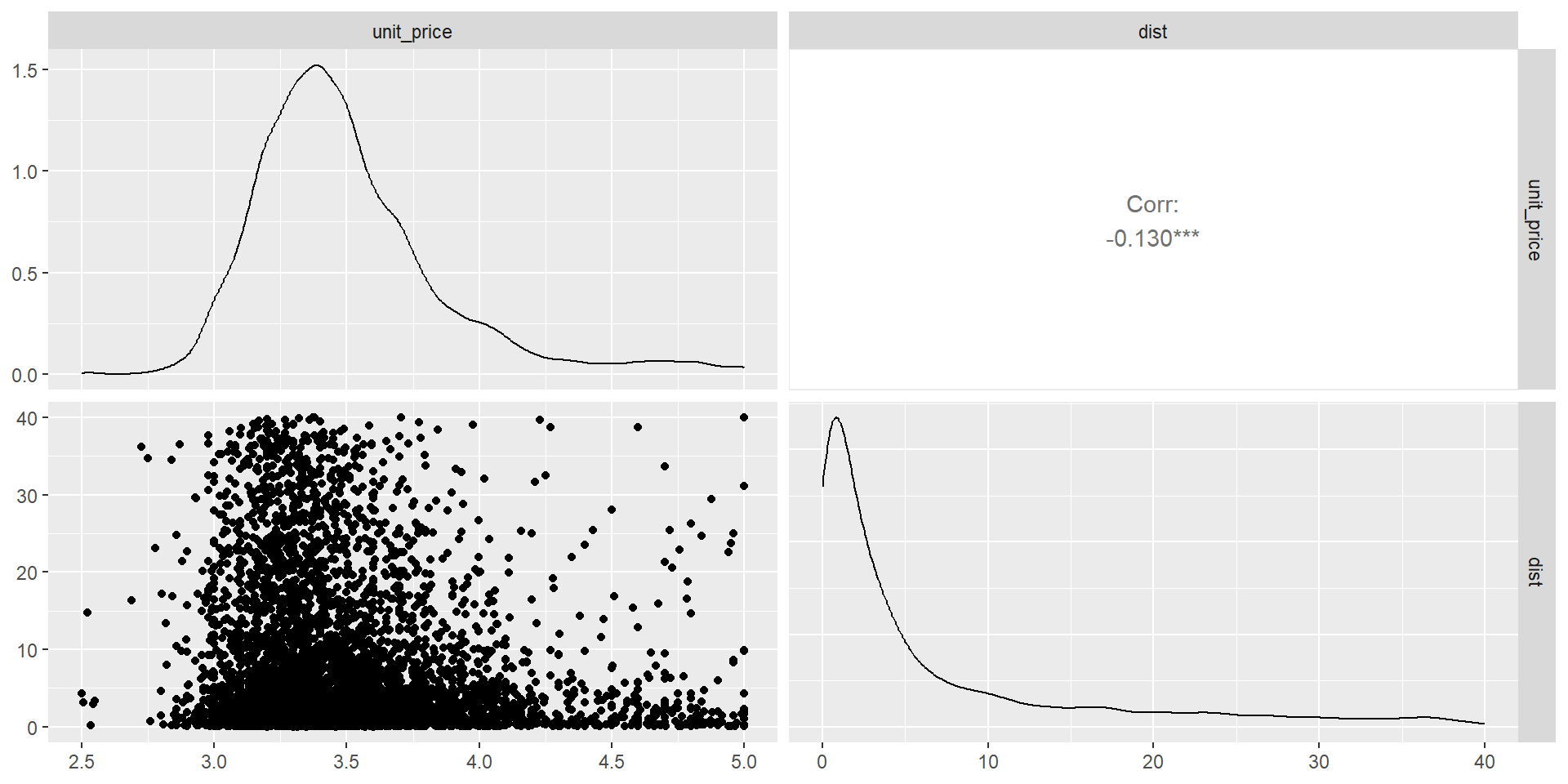
Unit prices appear to decrease as distance to highway increases
Figure 2: Scatter plot of unit price and distance
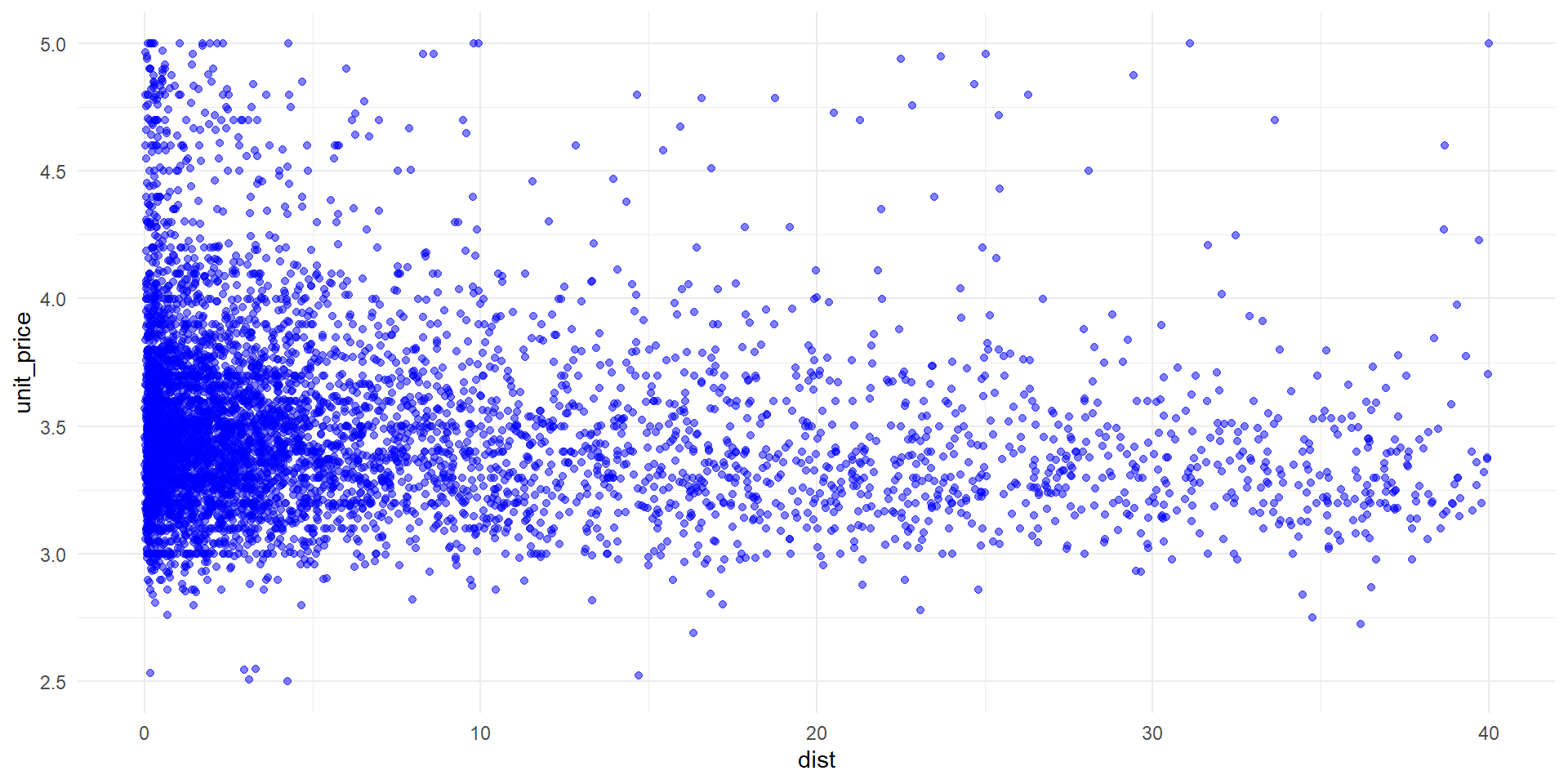
Univariate Regression Analysis
Although we can draw loose insights from the scatter plot, we use regression analysis to determine the relationship between distance and price.
\[ pr_{i} = \beta \cdot Dist_{i} + \alpha_i + \varepsilon_{i} \]
Outcome: price per gallon
Explanatory variable: distance to the highway (in kilometers)
Unit of observation: convenience stores with gas pumps
Univariate Regression Results
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 3.5344093 | 0.0057473 | 614.96894 | 0 | 3.5231426 | 3.5456761 |
| dist | -0.0052381 | 0.0005133 | -10.20554 | 0 | -0.0062443 | -0.0042319 |
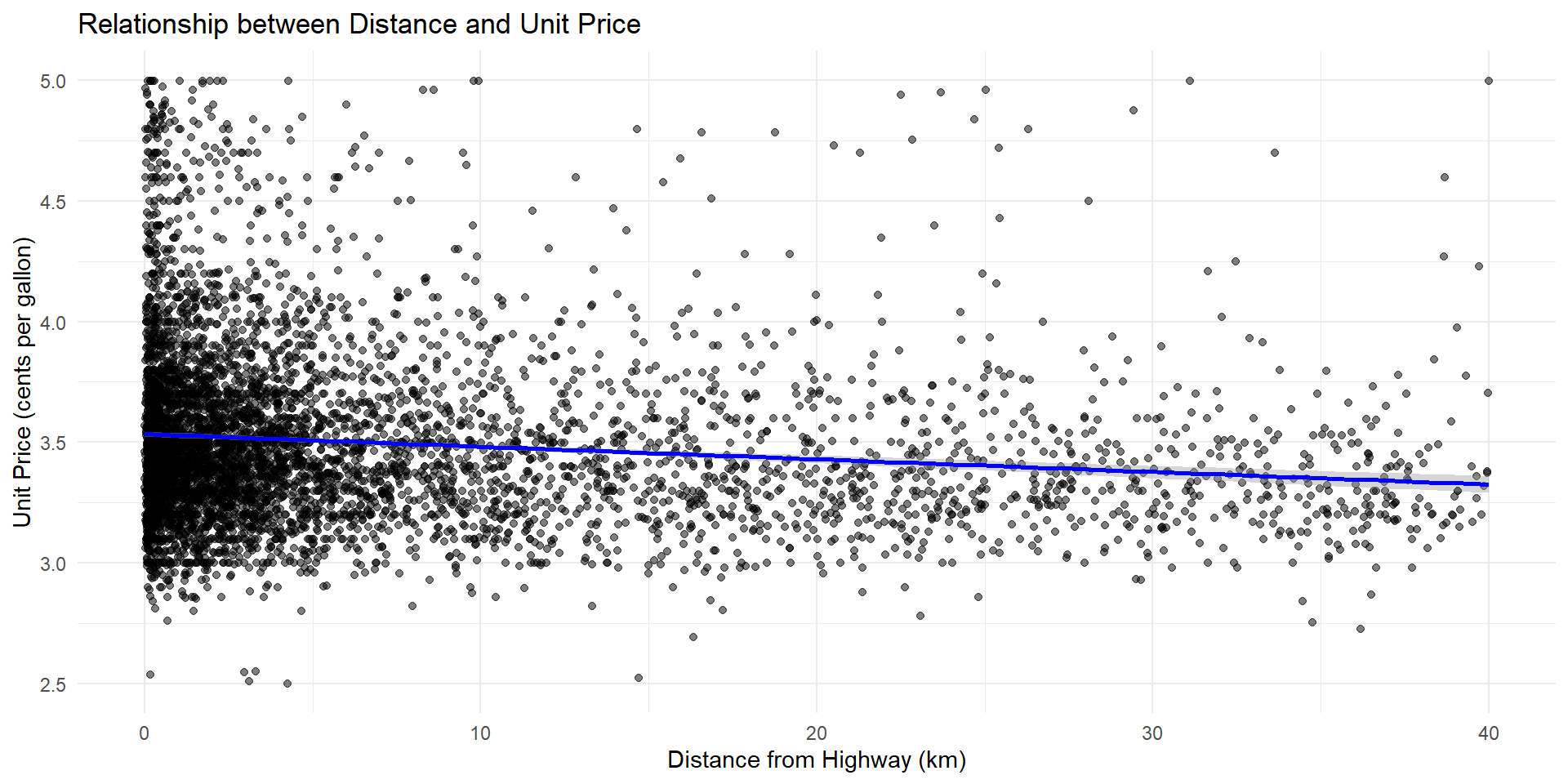
Our analysis shows a clear trend—each kilometer away from the highway corresponds with a decrease in gas prices.
For each additional km away from the highway, unit prices decrease by $0.005 cents per gallon
Figure 3: Scatter plot of unit price and distance, with line of best fit
Multivariate Regression Analysis
After adding additional control variables, we want to test if our results still hold.
\[ pr_{i} = \beta_1 \cdot Dist_{i} + \beta_2 \cdot X_{i} + \alpha_i + \varepsilon_{i} \]
Outcome: price per gallon
Explanatory variable: distance to the highway (in kilometers)
Controls: number of gas stations within 5 kilometers
Unit of observation: convenience stores with gas pumps
Multivariate Regression Results
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 3.5316728 | 0.0066272 | 532.9048492 | 0.0000000 | 3.5186811 | 3.5446644 |
| dist | -0.0051537 | 0.0005233 | -9.8489908 | 0.0000000 | -0.0061795 | -0.0041279 |
| count_within | 0.0012265 | 0.0014788 | 0.8293852 | 0.4069192 | -0.0016724 | 0.0041254 |
The p-value associated with the number of gas stations within 5 km is not statistically significant, so we cannot reject the null hypothesis that the coefficient is different from zero.
Takeaways
Our analysis shows consistent results between distance and unit price-each kilometer away from the highway corresponds with a decrease in gas prices.
Adding a control variable that attempts to capture competition (number of gas stations within 5 km) does not explain variation in unit prices.
Assumptions and Limitations
Assumptions:
We assume that a gas station will locate along the new highway access road (once it is built) near the highway to attract traffic flow from Highway 101.
We assume that gas stations compete uniformly along prices of their grades of gasoline.
Limitations:
We use distance “as the crow flies” versus travel distance along the road.
We do not account for other confounding factors that could influence gas prices, such as the traffic flow on Highway 101 nearest to the town and distance to the nearest major metropolitan area.
Discussion
The pattern we observe (inverse relationship between distance and price) suggests that stations closer to the highway charge a premium for the convenience of being located near the highway.
For those commuting to work places outside of town, this might mean higher travel expenses.
Conclusion
Our analysis confirms that distance from the highway is a key factor affecting gas prices in our community.
However, the considering the current travel cost to the highway without the access road, offsets the modest expected increase in gas prices.
Possible solutions:
Organize carpooling options
Support local gas stations with loyalty programs
Course Review
What was this course about?
Topics and themes
Effective and appropriate data visualizations
Data storytelling
Scripted data management and analysis (in R)
Organization
Time series
Cross sectional and spatial data
Regression analysis
What methods did we cover in these areas?
What is the purpose of decomposing a time series into its components?
A. To remove any anomalies or outliers from the data.
B. To prepare the data for regression analysis.
C. To determine the forecast accuracy of the time series.
D. To identify the underlying patterns and relationships within the data.
When is clustering analysis an appropriate technique for data analysis?
A. When the data is unlabeled or unstructured.
B. When the data has a clear target variable or outcome.
C. When the data has a linear relationship between variables.
D. When the data is in a time series format.
Which of the following analysis techniques is regression not suitable for?
A. Time series analysis
B. Unsupervised learning
C. Supervised learning
D. Difference in differences
How can color be used effectively in a data visualization?
A. To highlight important data points or trends.
B. To make the visualization more visually appealing.
C. To confuse the viewer with too many colors.
D. To distract from the key message of the visualization.
Our key takeaways from this course
Let the business or research question guide your analysis
Once you have something to say, develop a compelling story
Support your story with effective and appropriate visualizations